ペガサス
ニコニコミュニティ問題文
問題概要
\(N \times N\) マスの将棋盤と飛車と桂馬の動きを併せ持つ駒が \(N\) 個ある。お互いに取られないような \(N\) 個の駒の配置のパターン数を答えよ。
解法
駒は縦・横に自由に動けるので各行・各列に駒はひとつしかないことがわかります。
各列に対して何行目に駒があるかを考えるとこの問題は「\(1 \sim N\) の順列のうち隣の数字との差の絶対値が \(2\) にならないようなもの」を数える問題になります。
図: \(4 \times 4\) の例
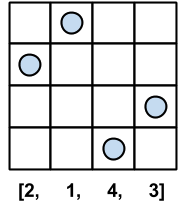
\(1 \sim n\) の適当な順列に \(n+1\) を挿入することを考えます。
- \(n-1\) の隣に挿入すると条件を満たさない隣接関係がひとつ発生します
- ただし \((n-3, n-1)\) が隣接してる場合、この間に挿入すると条件を満たさない隣接関係の総数は \(\pm\ 0\) になります
- \(n\) の隣に挿入しても条件を満たさない隣接関係は発生しません
- ただし \((n-2, n)\) が隣接してる場合、この間に挿入すると条件を満たさない隣接関係がひとつ解消します
- 上記以外で条件を満たさない隣接関係の間に挿入するとひとつ解消します
- それ以外の間に挿入しても条件を満たさない隣接関係の総数に変化はありません
以上を使い
\(dp[n][\)条件を満たさない隣接関係の総数\(][\)\((n-3,n-1)\)は隣接しているか\(][\)\((n-2,n)\)は隣接しているか\(] :=\) パターン数
というDPを更新していくと \(O(N^2)\) になります。
余談
王将と飛車という組み合わせだとA002464になります。これも \(O(N^2)\) で解けますが数列で考えると \(O(N)\) になります。ペガサスにも \(O(N)\) 解法がありそうな気もしますがよくわかりません。